Tree 개념

- 비선형 구조
- 원소들 간에 1:n 관계(계층 관계)를 가지는 계층형 자료구조
- 상위 원소에서 하위 원소로 내려가면서 확장되는 나무 모양 구조
트리의 특성
1. 한 개 이상의 노드로 이루어진 유한 집합
- 루트: 노드 중 최상위 노드
- 나머지 노드들: n(>=)개의 분리 집합 T1, ... , TN으로 분리 가능
2. 이들 T1, ... , TN은 각각 하나의 트리가 되며(재귀적 정의) 루트의 서브트리(SubTree)라고 한다.
트리의 구성요소
1. 노드(node): 트리의 원소
- 루트 노드: 트리의 시작 노드
- 형제 노드: 같은 부모 노드의 자식 노드들
- 조상 노드: 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드들
- 서브 트리: 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
- 자손 노드: 서브트리에 있는 하위 레벨 노드들
2. 간선(edge): 노드를 연결하는 선, 부모 노드와 자식 노드를 연결
3. 차수(degree)
- 차수: 노드에 연결된 자식 노드의 수
- 트리의 차수: 트리에 있는 노드의 차수 중 가장 큰 값
- 단말 노드(리프 노드): 차수가 0인 노드, 자식 노드가 없는 노드
4. 높이: 노드에서 루트에 이르는 길이, 노드의 레벨
- 트리의 높이: 트리에 있는 노드의 높이 중 가장 큰 값, 최대 레벨
Binary Tree
이진 트리의 특징
1. 모든 노드들이 2개의 서브 트리를 갖는 특별한 형태의 트리
2. 각 노드가 자식 노드를 최대한 2개 까지만 가질 수 있는 트리
3. 레벨 i에서의 노드의 최대 개수는 2개
4. 높이가 h인 이진 트리가 가질 수 있는 노드의 최소 개수는 (h+1)개, 최대 개수는 (2^(h+1) -1)개
이진트리 종류
1. 포화 이진 트리
- 모든 레벨에 노드가 포화상태로 차 있는 이진 트리
- 최대의 노드 개수인 (2^(h+1) -1)의 노드를 가짐
- 루트를 1번으로, (2^(h+1) -1)까지 정해진 위치에 대한 노드 번호를 가짐
2. 완전 이진 트리
- 높이가 h이고 노드 수가 n개일 때, Full 이진 트리의 노드 번호 1번 까지 빈 자리가 없는 이진 트리
3. 편향 이진 트리
- 높이 h에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드 만을 가진 이진 트리
순회
1. 순회: 트리의 각 노드를 중복되지 않게 전부 방문
2. 트리는 비선형 구조이므로 선형구조에서와 같이 선후 연결 관계를 알 수 없다.
3. 순회방법
- 전위순회: 자손노드보다 루트노드를 먼저 방문
# 현재 노드 n을 방문하여 처리: V
# 현재 노드 n의 왼쪽 서브트리로 이동: L
# 현재 노드 n의 오른쪽 서브트리로 이동: R
def preorder_traverse(T):
if T: # T is not None
visit(T) # print(T.item)
preorder_traverse(T.left)
preorder_traverse(T.right)
- 중위순회: 왼쪽자손, 루트, 오른쪽 자손 순으로 방문
# 현재 노드 n의 왼쪽 서브트리로 이동: L
# 현재 노드 n을 방문하여 처리: V
# 현재 노드 n의 오른쪽 서브트리로 이동: R
def inorder_traverse(T):
if T:
inorder_traverse(T.left)
visit(T)
inorder_traverse(T.right)
- 후위 순회: 루트노드보다 자손을 먼저 방문
# 현재 노드 n의 왼쪽 서브트리로 이동: L
# 현재 노드 n의 오른쪽 서브트리로 이동: R
# 현재 노드 n을 방문하여 처리: V
def postorder_traverse(T):
if T:
postorder_traverse(T.left)
postorder_traverse(T.right)
visit(T)
Expression Tree
리스트를 이용한 이진 트리의 표현
- 노드 번호가 i인 노드의 '부모노드' 번호 = | i / 20 |
- 노드 번호가 i인 노드의 왼쪽 '자식노드' 번호 = 2 * i
- 노드 번호가 i인 노드의 오른쪽 '자식노드' 번호 = 2 * i + 1
이진 탐색 트리(Binary search Tree)
1. 이진탐색트리 특징
- 탐색 작업을 효율적으로 하기 위한 자료구조
- 모든 원소는 서로 다른 유일한 키를 가짐
- key(왼쪽 서브트리) < key(루트 노드) < key(오른쪽 서브트리)
- 왼쪽 서브트리와 오른쪽 서브트리도 이진 탐색 트리
- 중위 순회하면 오름차순으로 정렬된 값을 얻을 수 있다.
2. 탐색 연산
- 루트에서 시작
- 탐색할 키값 x를 루트 노드의 키값과 비교
- 서브트리에 대해서 순환적으로 탐색 연산 반복
3. 삽입 연산
- 먼저 탐색 연산 수행
- 삽입할 원소와 같은 원소가 트리에 있으면 삽입 불가, 같은 원소가 트리에 있는지 탐색하여 확인
- 탐색에서 탐색 실패가 결정되는 위치가 삽입 위치가 된다.
- 탐색 실패한 위치에 원소 삽입
Heap
완전 이진 트리에 있는 노드 중 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해 만든 자료구조
|
최대힙 |
최소힙 |
|
- 키 값이 가장 큰 노드를 찾기 위한 완전 이진트리 - {부모 노드 키 값 > 자식 노드 키 값} - 루트노드: 키 값이 가장 큰 노드 |
- 키 값이 가장 작은 노드를 찾기 위한 완전 이진트리 - {부모 노드 키 값 < 자식 노드 키 값} - 루트노드: 키 값이 가장 작은 노드 |
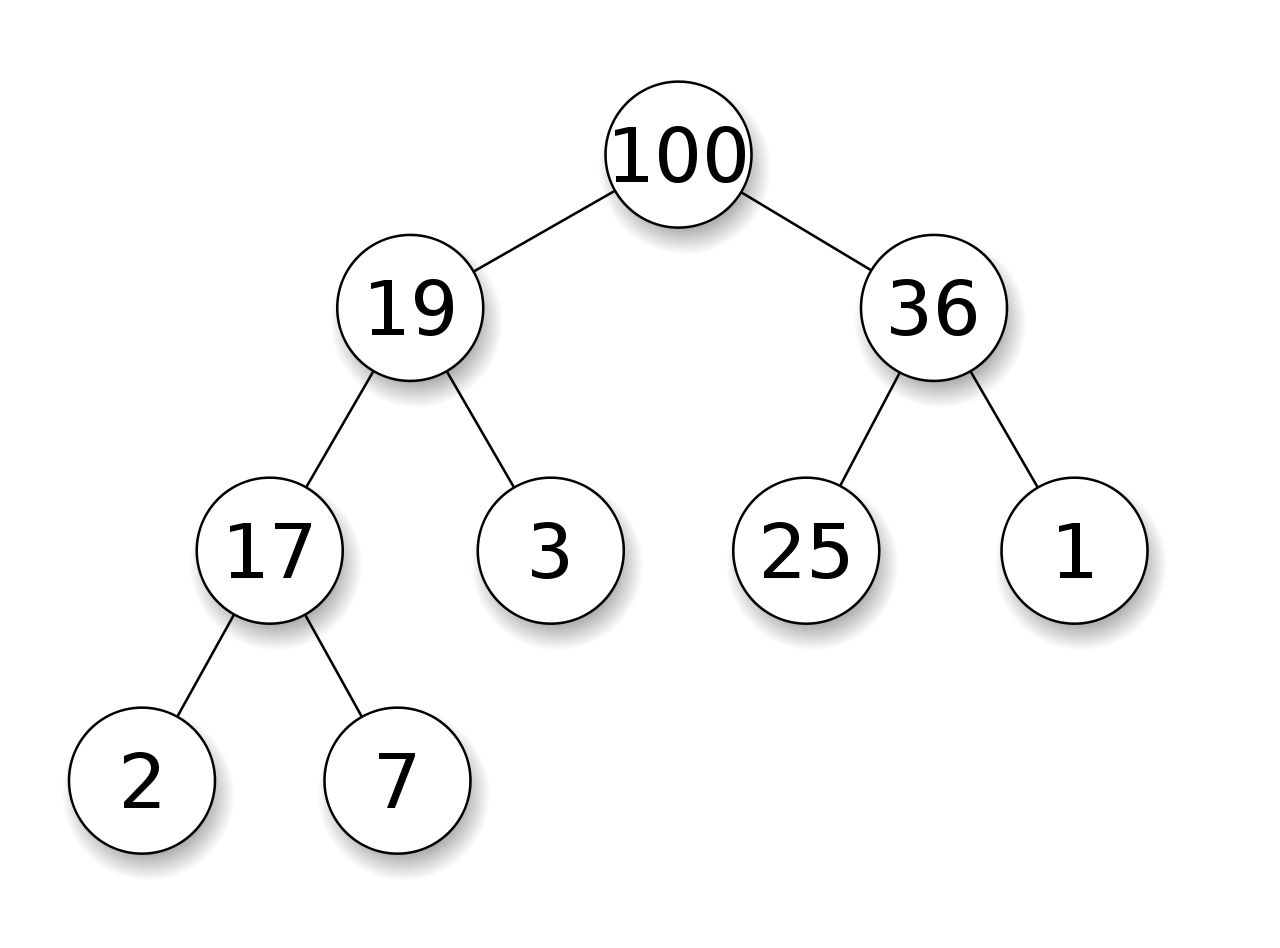
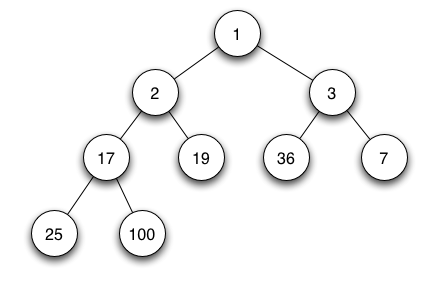
힙 연산
1. 삽입 연산
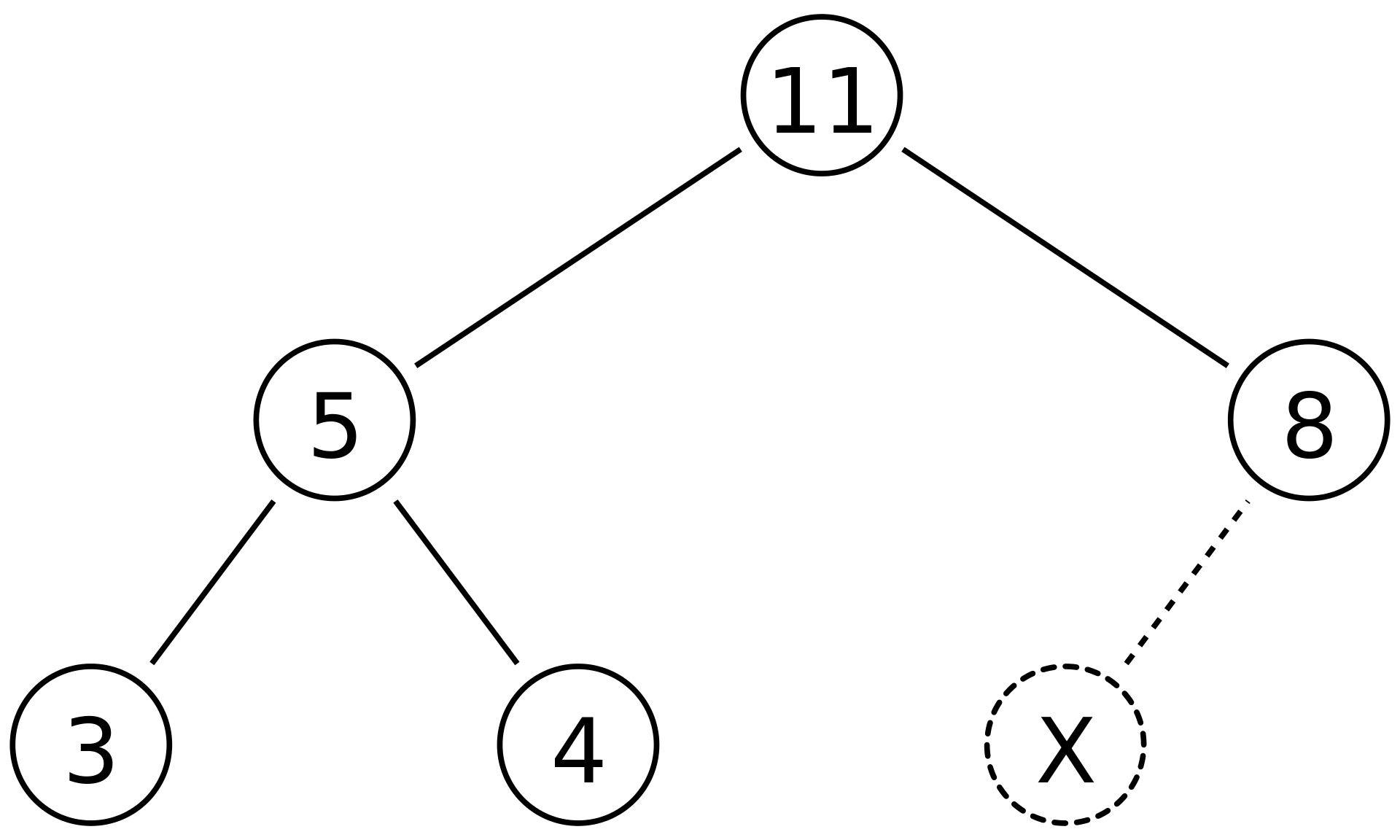
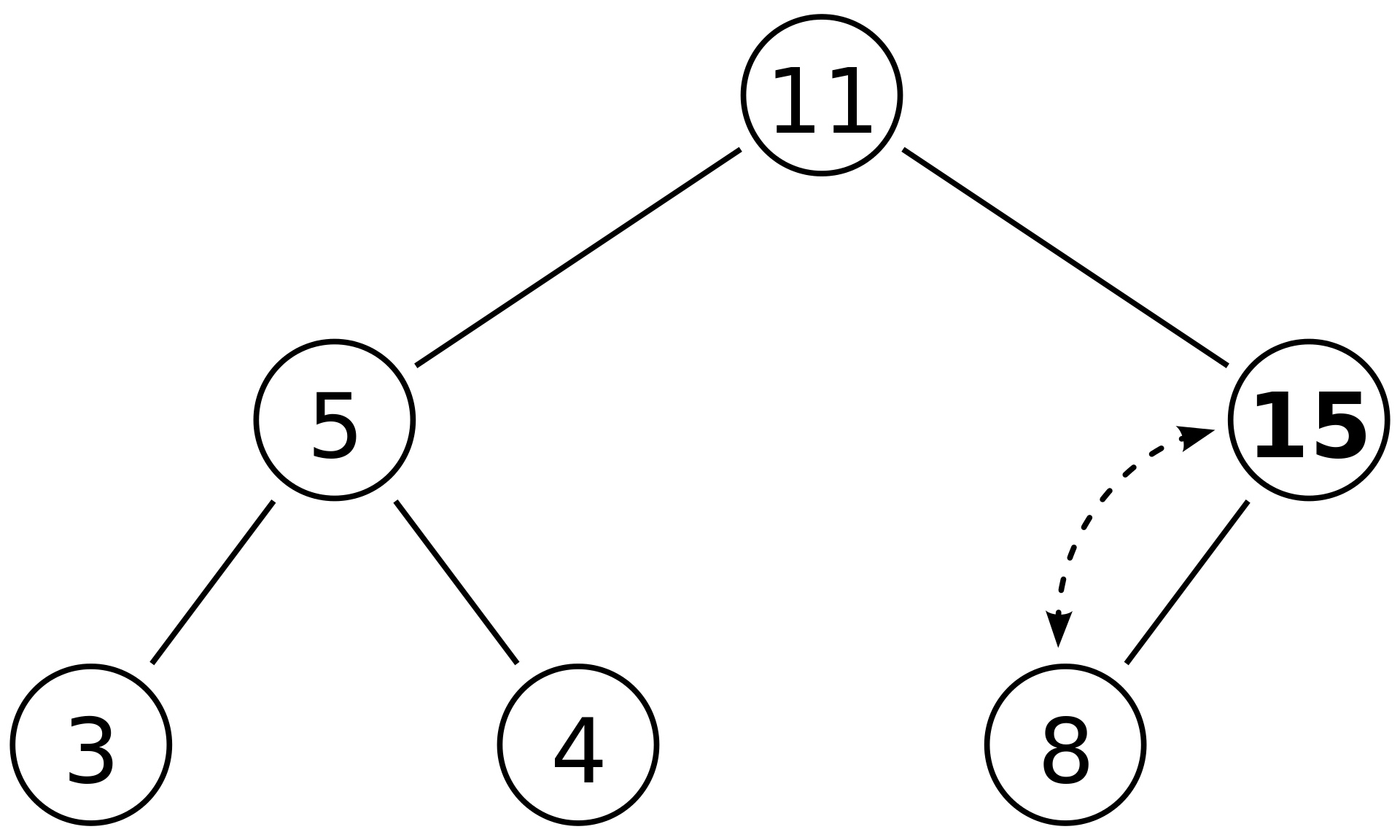
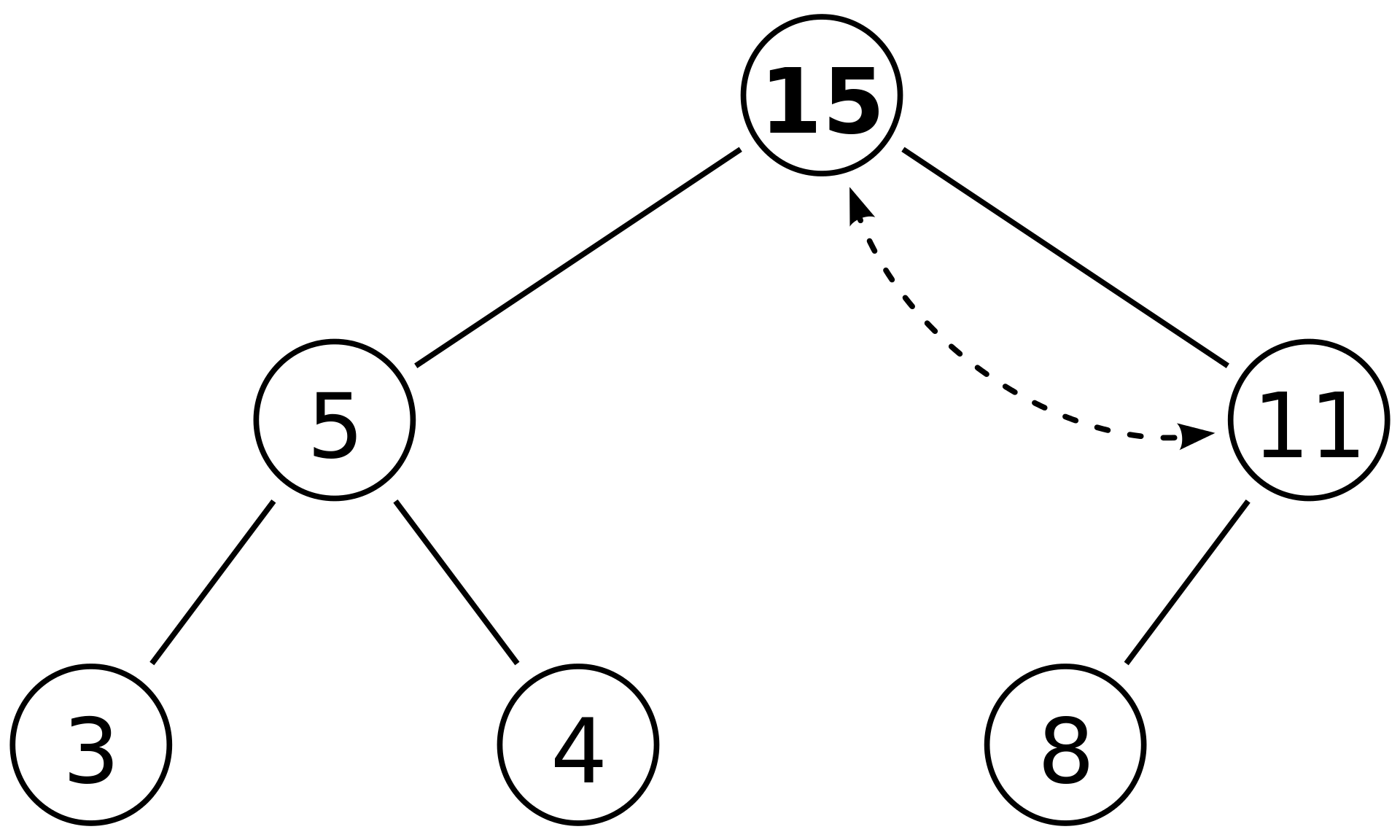
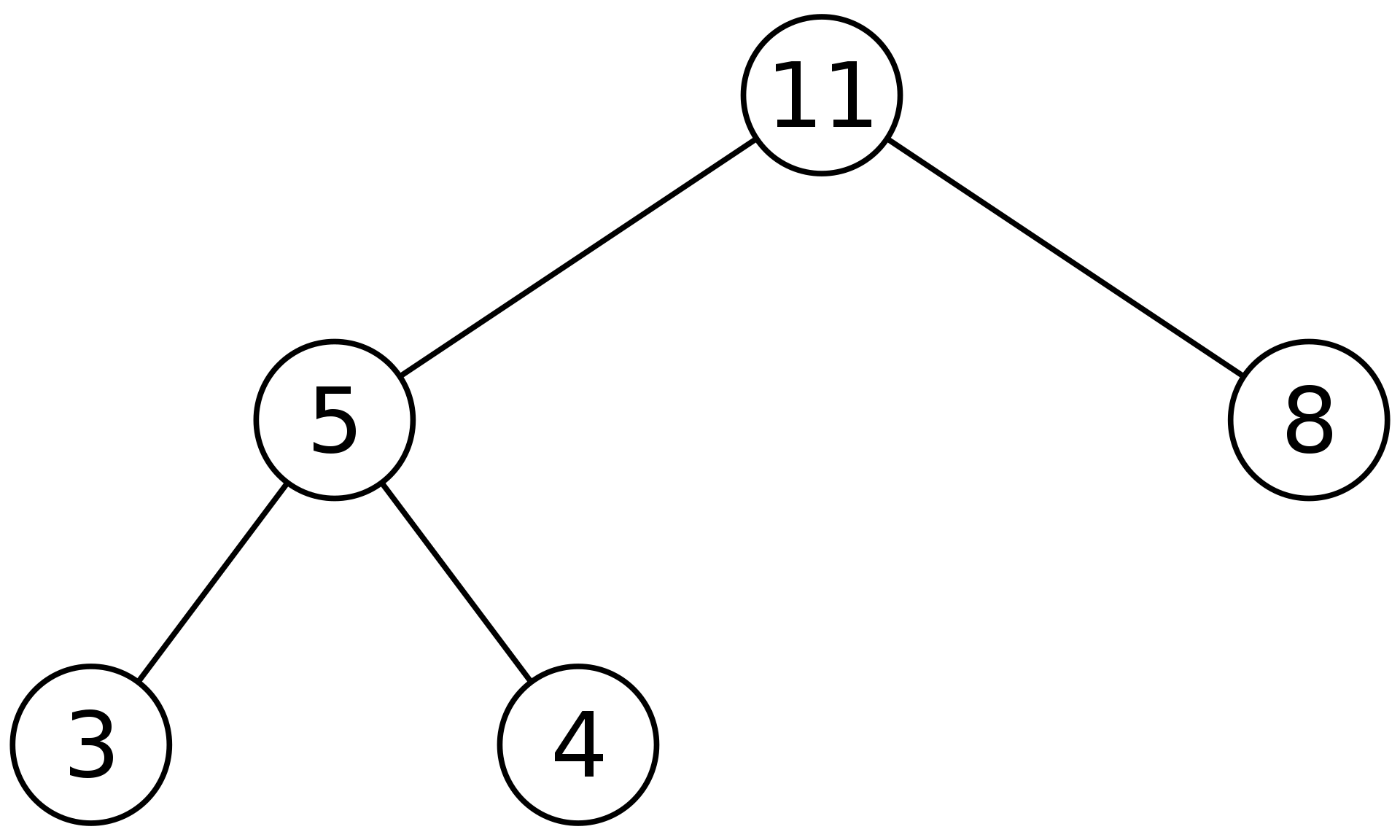
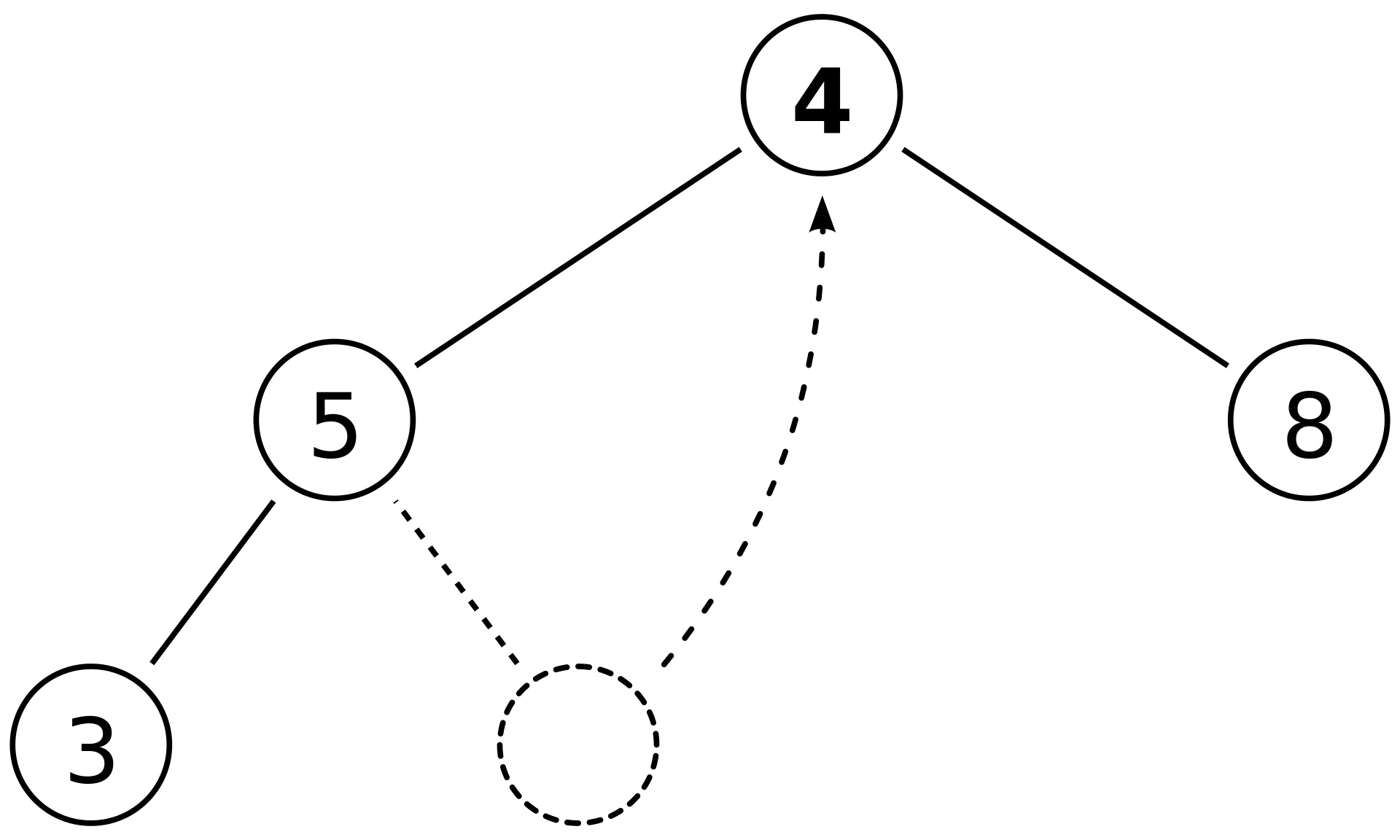
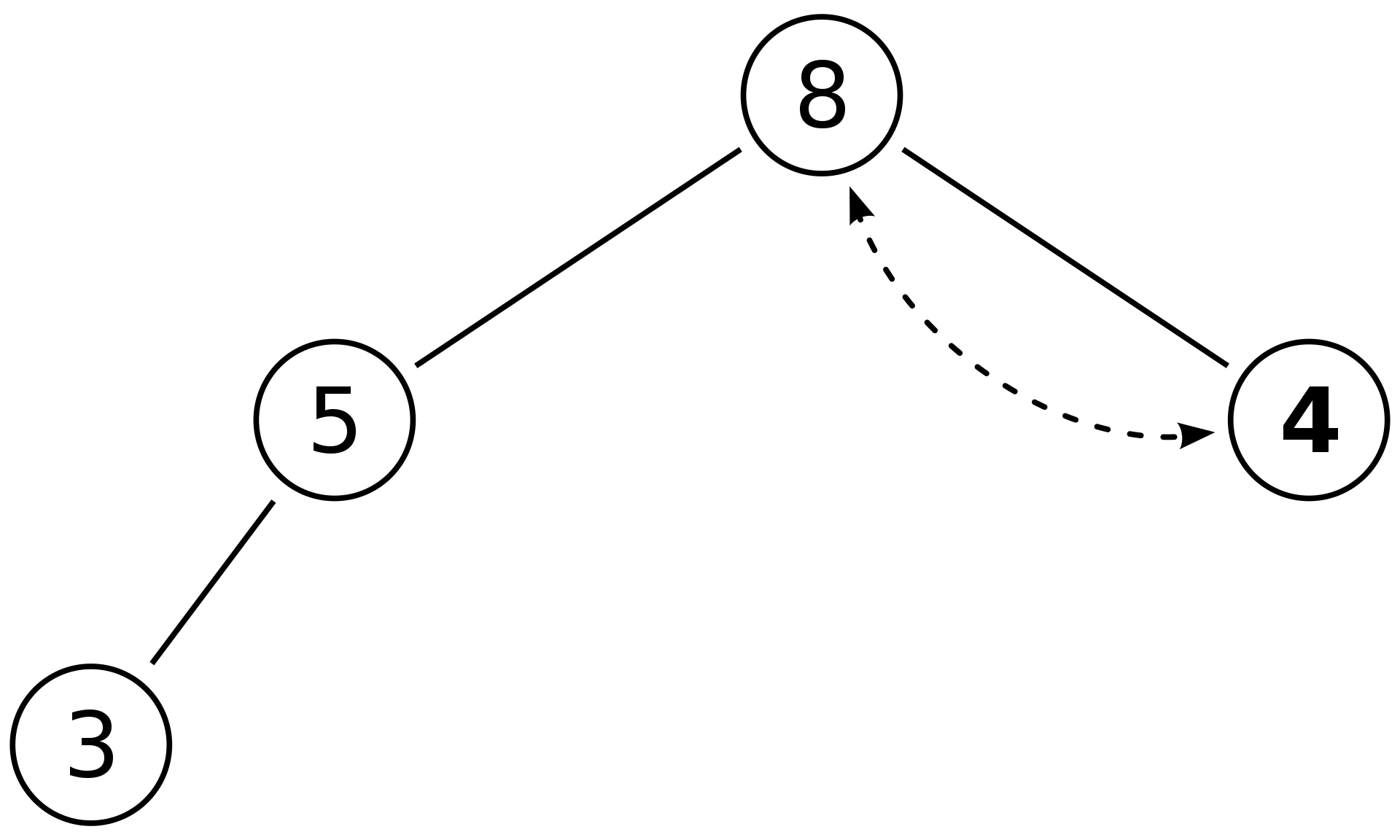
2. 삭제 연산
- 힙에서는 루트 노드 원소만 삭제 가능
- 루트 노드 원소만 삭제하여 반환
- 힙 종류에 따라 최대값과 최소값을 구할 수 있다. -> 우선순위 큐를 힙으로 구현 가능
'인문학도 개발일지 > 1일1알고리즘' 카테고리의 다른 글
| [python] *sorted 파이썬 아스테리스크/백준2750번 (0) | 2021.02.11 |
|---|---|
| [python] continue와 pass의 차이 (0) | 2021.01.27 |
| [알고리즘] 코드업 1060 파이썬: 비트단위로 AND 하여 출력하기 (0) | 2020.05.08 |
| [알고리즘] 백준 알고리즘: 10718번 We love kriii 코틀린(Native) 풀이 (0) | 2020.04.16 |
| [알고리즘] 백준 알고리즘: 2557번 Hello World! 코틀린(Native) 풀이 (0) | 2020.04.16 |





